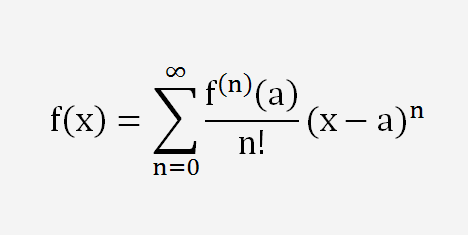 在YouTube上看到了一段教数学的视频,就是台湾那个老师讲的。内容是泰勒展开式入门(http://www.youtube.com/watch?v=XXnAoC7BW6k),其中有一些话颇有意义。
在YouTube上看到了一段教数学的视频,就是台湾那个老师讲的。内容是泰勒展开式入门(http://www.youtube.com/watch?v=XXnAoC7BW6k),其中有一些话颇有意义。
如果一个函数如果可以用等号后面的东西表示出来的话,那么这个函数就是说,可以用泰勒展开式的方法展开来的。
在人类历史上,人类对泰勒展开式的兴趣之所以那么高,完完全全是因为(x-a)的n次方,(x-a)的n次方是多项式,多项式是当时人类最熟悉的函数形式之一。
但是在比较高等的数学里,我们有兴趣的完完全全是f(x)在a处的n阶导数这一项。这个n阶导数完全刻画出了泰勒展开式最重要的一个特征,叫做:“一叶知秋”。什么叫做“一叶知秋”,就是说一片叶子掉下来,我就知道秋天到了。好,f(x)在a处的n阶导数,导数的定义是什么,导数的定义是在x趋近于a的时候在a的临域所发生的事情。f(x)在a处的n阶导数就是它的一阶变化率,二阶变化率,三阶变化率... 但是呢,它始终是在a的旁边一点点。我只要知道a点附近的这些东西,除以n的阶乘,再乘以(x-a)的n次方,我就完完全全可以知道函数在整个坐标系里的行为是什么,就知道了这个函数是什么。也就是说,我只要得到a附近的一点点的信息,我就可以知道这个函数长什么样子。
不只是这些,a还可以动,也就是说,函数上任意一点的临域都包含着函数的全部讯息!这就是泰勒展开式最重要的意义。
事实上泰勒展开式所研究的函数的种类,是数学上很稀少的一类,叫做解析函数。
我们的人生是解析函数吗?如果是的话,我们可以在最短最短时间内我们所经历的一切,外推到整个人生。所以说,如果人生是解析函数的话,那就太棒了。我们只要活一点点,我们就可以用一点点的生涯去幻想无穷无尽的生命到底是长什么样子。
有一个我很敬佩的数学家,他说过一句话,“死并不可怕,死只是我所遇到的最后一个函数”。意思就是说,其实他认为人生并不是解析函数,他在那个时候已经认识到了,人生是充满着断点,跳跃,以及不连续点,人生是一个非常非常算是 正规 的函数。因为事实上,Weierstrass已经证明:处处连续但处处不可微分的函数才是函数的常态。